Normal Distributions

-

 For a long time ,I always wondered what those crazy looking curves actually meant ,what were its significance ,it's applications. Today let's figure it out .


Distributions are important because just by looking at the shape of distribution formed by the data ,one can draw a lot of insights without even actually going through the data .

A distribution is simply a collection of data, or scores, on a variable. Usually, these scores are arranged in order from smallest to largest and then they can be presented graphically.

                                — Page 6, Statistics in Plain English, Third Edition, 2010.

Gaussian / Normal  Distribution:

Have you ever wondered why all new born babies are "almost" of same heights if not exactly ?? Yes there may be exceptions where a baby is somewhat taller or dwarf than rest. Also have you ever wondered why most of the students in a class are roughly of same height ,and very few will be extreme tall or dwarf  ? Did you ever thought why in any given exams many students gets grade A and  B , very few get A+ and C. If not, no worry ,I also never wondered ?? But let's talk about it now.

Normal Distribution is defined by following equation.



Do not worry by this crazy looking equation , it can simply be represented by exponential of some squared term which we have already studied sometime in past.

Image by Author


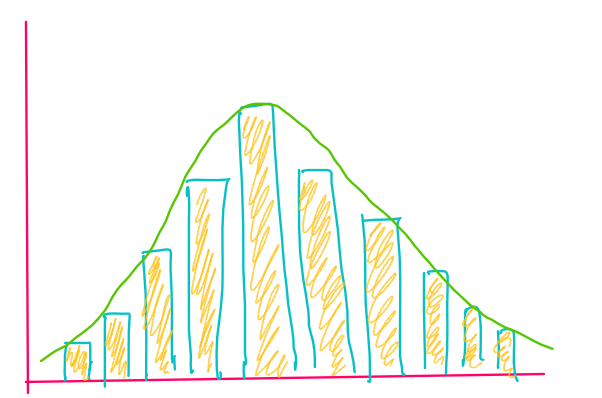
As we can see in the figure it becomes very much obvious why Normal Distribution is often called Bell Curve ,because it looks as bell. On the y axis we can see the probability where "More Likely " lies near 1 and "Less Likely " lies near 0 . Reminder probability lies between 0 and  1. Most of the data tend to cluster around the center value and further the value is away from center ,less likely  it is to occur.

Let's go with an example below , here we can see two distribution one is of Babies heights and other is of Students heights in a class. It is very much evident that babies height is lesser as well as all babies are almost of same sizes therefore the distribution is very much peaked around value 20 inches.
Whereas in a class of student we can find students with different heights mostly  of same heights around 70 inches and correspondingly less students who are taller or shorter.

Original Image by StatQuest with Josh Starmer 



The mean value of the babies is 20 inches whereas that of students is 70 inches. As we can see from the image ,we can infer that the Normal Distribution is always centered at mean value
You may question why curve for babies is taller than that of curve for students, it is just because there are many possibilities for heights of students than of babies .

Variance is the spread of the data that is how data is spread around the mean.


We generally don't talk about variance because it doesn't hold the unit as that of  mean so we cannot plot both the value over same curve. By saying that they don't have same units, what I meant is let's say we found mean of height of students as 180 cm ,but after finding it's variance ,as there is a square term in its formula , it's unit will become cm squared ,so we cannot plot them over same plot 


The width of the curve formed by yellow rectangle shown in the figure  is defined by standard deviation .Standard deviation is important parameter because normal distribution is drawn such that  around  68% of measurements falls between +/- 1 standard deviation ,95% of measurements falls between +/- 2 standard deviation and 99.7% measurements falls between +/- 3 standard deviation .


Standard deviation is the square root of Variation and therefore is mostly used with the mean as they both have same unit.

Wikipedia



Remember that spread of the curve determines how tall the curve can be ,that is if curve has high spread ,it will be shorter , if curve has less spread then it will be taller. 

Real Life Applications:
  • Measurement errors in physical experiments are often modeled by a normal distribution.
  • Many scores are derived from the normal distribution, including percentile ranks ("percentiles" or "quantiles")
  • In hydrology the distribution of long duration river discharge or rainfall, e.g. monthly and yearly totals, is often thought to be practically normal
  • In standardized testing, results can be made to have a normal distribution by either selecting the number and difficulty of questions  or transforming the raw test scores into "output" scores by fitting them to the normal distribution.

Take Away points:

  • Normal Distribution has two parameters mean and standard deviation
  • It is centered around mean
  • 68% of measurements falls between +/- 1 standard deviation
  • 95% of measurements falls between +/- 2 standard deviation 
  • 99.7% of the data falls in the range of +/- 3 standard deviation 

References:

Comments

Post a Comment

Popular posts from this blog

Covariance and Correlation

-
Image
While dealing with any ML project one spends most of the time in data preprocessing .Data pre-processing is nothing but playing with the features present in the dataset ,data cleaning,data transformation ,removing or imputing missing feature values etc. Feature engineering corresponds to developing  new features based on current information . It may happen that few features are related to each other be it directly or inversely . Consider three cases:  Let's say radius and circumference are features present in the dataset ,so we know that they are directly dependent .Here if radius increases ,perimeter also increases.       2. Let's say speed and time are features present in the dataset ,so we know that they are inversely               proportional  .Here if speed increases ,time required to cover a distance decreases.         3. Let's say height and hair color are features present in the datas...
Read more

Split it up - Part 1

-
Image
M achine  L earning ???? How can a machine even learn??  For a long period of time I always wondered what this fancy term meant and how would it be actually possible ..!! Let's figure it out today. To get an essence of what happens when we say Machine is learning ,why not understand in the first place how we learn. Well..!!! let us take a glance at those days when we learnt mathematics as a kid. I still remember how my maths teacher used to teach us basic addition and subtraction in class .Initially she helped us to count using fingers and then add or subtract those numbers. With a lot of practice and sometimes getting beaten up by her we finally learnt addition /subtraction. Mathematically speaking after lot of practice /training , our brain learnt a function of addition where if we get numbers to add ,it processed in a way to give the sum. Similarly Machine Learning is all about finding that magic function "f" wherein ,we give some input and desire some output . (EXC fo...
Read more

Why activation function is needed in Neural Networks???

-
Image
Today allow me to share with you, the relationship between a spider and an activation function   Activation function is used in Neural network to introduce the non-linearity. Without the proper activation function, neural network will simply be large Linear Model.   Consider the case where you have a data which is linearly separable  Constructing a model to separate yellow and orange data points is very simple. A simple logistic regression will do this job very perfectly  Now consider the case where your data set looks like something shown below What do you think now?? will a simple linear model be able to carve out the hyperplane in such a way to classify both yellow and orange points. I don’t think so. And it is the fact that a simple linear model may not be able to find complex patterns in a data.  So now we go to big brother of linear model -Neural network. Neural Network has this super ability to both carve out linear...
Read more