Mathematical Formulation for Logistic Regression
Today we will explore the mathematical backing of the Machine Learning Algorithm LOGISTIC REGRESSION. I hope you are already well acquainted with the theory behind it. Let’s dive deep inside the pool of mathematics to know what goes behind logistic regression.
As we know Logistic Regression is a binary classifier, consider a two class classification problem consisting of red and blue as two classes, and are separated by a straight line. We assume that our data is linearly separable.
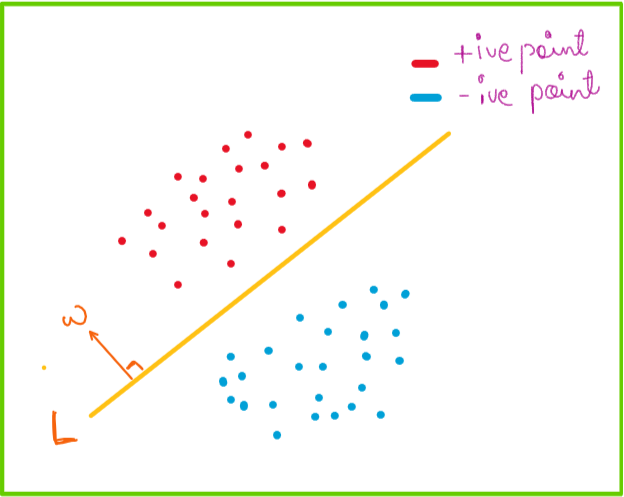
The line L has a normal w and intercept b. Original direction of normal to the line is towards red points. If the L passes through origin then b equals 0. We know that a line can be represented in the form of its normal is L: wt*x +b=0 where w is a vector, x is a vector and b is a scalar
Now the problem statement is given the data points consisting of red and blue points, we need to find such a line with w and b that separates red points from blue points. How can we approach this problem??
Let’s see… First try to understand the data, as already discussed it is linearly separable. Secondly understand the classes present in the data . We consider -1 as blue data points and +1 as red points, i.e. yi = +1 for red points and yi = -1 for blue points.
In order to find the best line to separate this points from each other we start by choosing a line with random orientation, i.e. any value of w and b. Let’s say now I choose a query point xqi in the red points, then the distance between this point and the line L will be di and similarly consider a query point xqj in blue points whose distance from line L is dj . For the sake of simpler calculation we consider line to be passing through origin, which implies b=0.
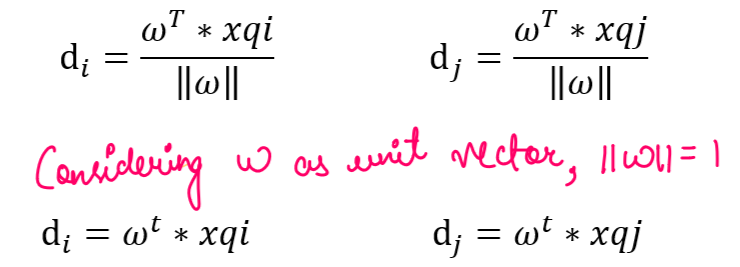
We consider that our w is unit vector which basically means norm(w) =1. As I said we consider vector w towards red points initially, so its direction towards blue point is by default in negative direction. Hence the distance of line L from query point xqj is negative.
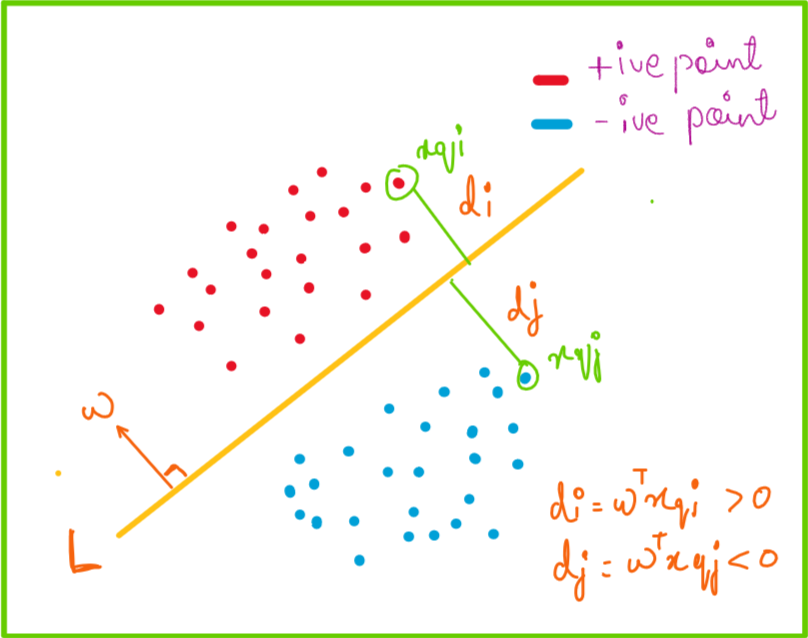
We say that our classifier is correctly classifying the data points when the actual point’s class and the class found out by our model is same, which basically implies if point is positive yi=+1 and model also predicts it to be +1 when wt*xqi >0, similarly if the actual point is negative yj = -1 and model predicts it to be -1 when wt*xqj <0 .
Other case can be when our classifier is incorrectly classifying the data points when the actual point’s class and the class found out by our model is different , that is, if point is positive yi=+1 and model also predicts it to be -1 when wt*xqi <0, similarly if the actual point is negative yj = -1 and model predicts it to be +1 when wt*xqj >0.
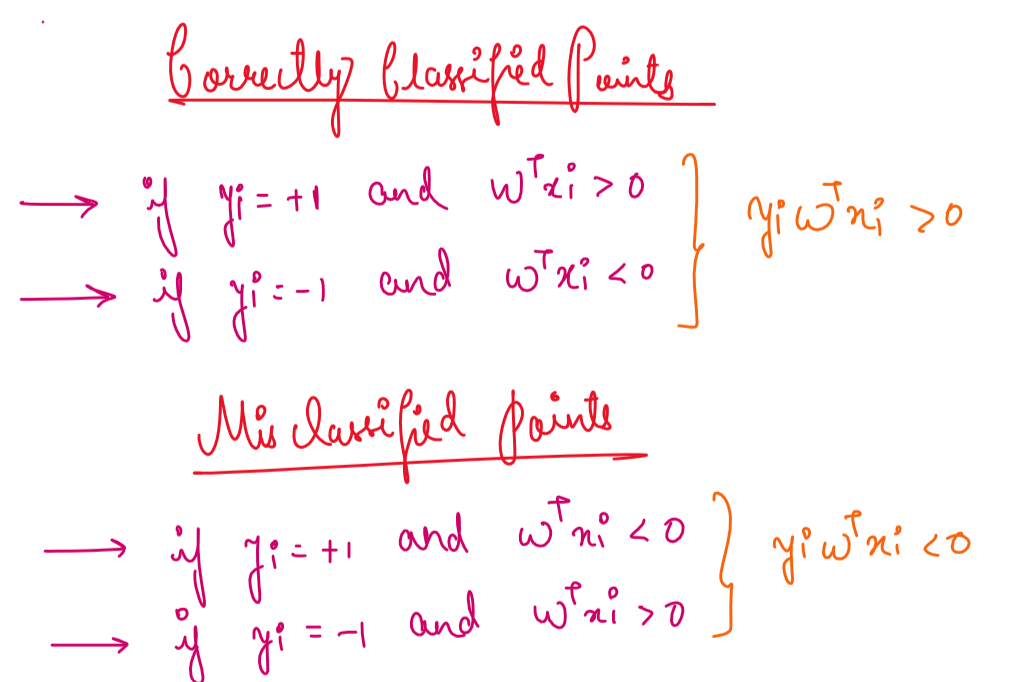
Intuitively the best model will be the one which has maximum correctly classified points, which is defining our optimization problem. Over here our optimization problem is to find such a combination of w and b which will maximize the correctly classified points.
But here the problem is as this is a distance based approach if some positive point lies in other side of the line that too a great distance which basically means a outlier, due to huge distance it may not be able to create a suitable line or hyper plane, that is why we use a popular function called Sigmoid Function which basically squeezes the whole function into a range of 0 and 1.The extra large positive values squeezes to +1 and extra large negative values squeezes to 0 and rest lies between 0 and 1.
Now we apply sigmoid function to our optimization problem which results in following result.
To make calculation simpler, we apply log to this overall function, and you might ask why only log, so answer to this question is, it is monotonically increasing function and our optimization problem is also monotonically increasing function so it eases calculation when we apply log over top of optimization function as shown below.As of now our total function has become negative and we have maximization problem initially so overall it becomes a minimization problem after removal of minus sign.
Let me summarize the above equation for you
find an optimal w such that it will minimize the optimization function in order to find the line/plane such that, it maximizes the prediction of correctly classified points.
Just for sake of simplicity we took a 2d data and have a line to separate them. But in real world you will have high dimension data and for that you will need a hyperplane to separate the data points.
As after training we get an optimal set of w and b. Now if you take a query point xq which is present in let's say in red points then models has already learnt the w vector, so it will simply find wt*xq and then apply sigmoid on it, if it's value is greater than some threshold let's say 0.5 then it will be considered as positive point else negative point.
That's it for this time, hope ypou got the essence of mathematics envolved in Logistic Regression
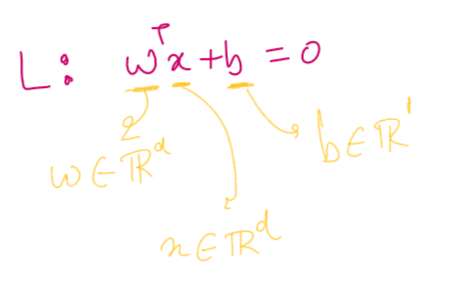





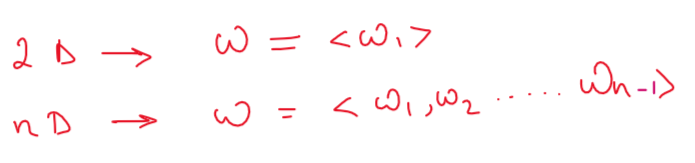




Comments
Post a Comment